Elements of Symmetry

Session Objectives

By the end of this
session, students will be able to:

• What are elements of symmetry?

• Types of symmetry

Symmetry
and Stereochemistry

• There are three elements of symmetry that a
molecule may possess…

1. Rotation

2. Reflection

3. Inversion

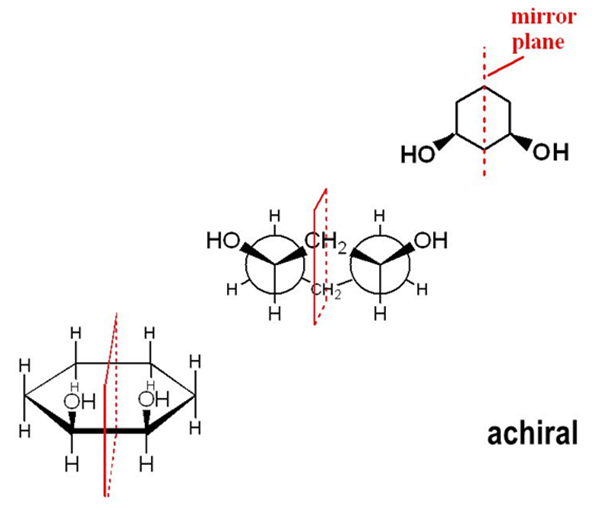
Symmetry Operations: Reflection

• Symmetry
operations are spatial transformations (rotations,
reflections, inversions).

• A molecule is said to possess a symmetry element if the
molecule is unchanged in appearance after applying the symmetry operation
corresponding to the symmetry element.

• The blue plane is a plane of symmetry of A.

• The operation of reflection (М) involves projection
of each atom onto the plane, followed by movement through the plane to a
distance equal to the projection distance.

• Reflection through the plane is a symmetry operation on A.

• Although the red and
magenta H’s have changed places, the
molecule looks the same.

• We say that A possesses reflection symmetry.

• Animations of the reflection process

Elements
of symmetry

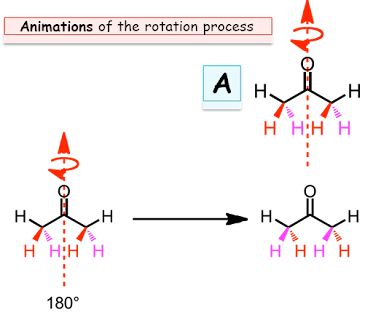
Symmetry Operations: Rotation

• A molecule is said to possess a symmetry element if the
molecule is unchanged in appearance after applying the symmetry operation
corresponding to the symmetry element.

• The red axis is an axis of symmetry of A.

• The operation of rotation (C_n) involves
rotation of the molecule 360/n degrees about an axis.

• The axis shown is a “C₂” axis.

• Rotation about the axis is a symmetry operation on A.

• Although the red and magenta H’s have changed places, the
molecule looks the same.

• We say that A possesses 2-fold rotational symmetry.

Elements
of symmetry

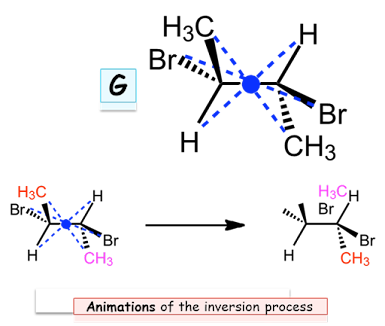
Symmetry Operations: Inversion

• A molecule is said to possess a symmetry element if the
molecule is unchanged in appearance after applying the symmetry operation
corresponding to the symmetry element.

• The blue point is an inversion center of G.

• The operation of inversion (i) involves the
projection of each atom onto a point at the center of the molecule, followed by
movement through the point to a distance equal to the projection distance.

• Inversion through the point is a symmetry operation on
G.

• Although inversion exchanges all three groups attached to
the central carbon, the molecule looks the same. We say that G possesses
inversion symmetry.

Alternating
axis of symmetry (Sn) or Rotation reflection axis of Symmetry or improper axis
of Symmetry

• A molecular has an alternating axis of symmetry of order
(n) if rotation about the axis by 360/n degree following by reflaction in a
plane perpendicular to this axis produces an equivalent structure.

Summary

• Chirality is only the criteria for optical isomerism

• The molecule should lack these elements of symmetry to
possess optical isomerism

• Different types of symmetry

        Plane of
symmetry – reflection

        Axis of
symmetry – rotation

        Centre of
symmetry – inversion centre

        Alternating
axis of symmetry