Compartment Modelling Intravascular and Extravascular

Compartment Modelling Intravascular and Extravascular

Contents

• Introduction
• Compartment modeling
• One-compartment open model
• One-compartment open model for IV bolus

Session objectives

By the end of this lecture, students will be able to:

• Explain the concept of modeling in bio-pharmaceutics and pharmacokinetics
• Discuss the advantages and disadvantages of different compartment modeling
• Estimate pharmacokinetic parameters for intravascular and extravascular administration from single and multi-compartment models
• Describe the differential equations for a simple pharmacokinetic model for open IV bolus administration

Mathematical model

• A model is a mathematical description of the biological system and is used to express quantitative relationships.
• Mathematical models are a collection of mathematical quantities, operations, and relations together with their definitions and they must be realistic and practical.
• A model is a hypothesis that employs mathematical terms to concisely describe quantitative relationships.

Why model the data?

There are three main reasons due to which the data is subjected to modeling:

1. Descriptive: to describe the drug kinetics in a simple way
2. Predictive: to predict the time course of the drug after multiple dosing based on single-dose data, to predict the absorption profile of the drug from the iv data.
3. Explanatory: to explain unclear observations.

Qualities of a mathematical model

Validity: It should have practical applicability and should be valuable in describing events chosen accurately with high precision

Prediction ability: These models predict the qualitative and quantitative changes in these parameters that are rate constants and half-lives of drugs

Computability

Consistency of results: Reproducibility is an important quality of a mathematical model

Applications of pharmacokinetic model

• Characterizing the behavior of drugs in patients
• Calculating the optimum dosage regimens for individual patients
• Evaluating the bioequivalence between different formulations of the same drug
• Determining the influence of altered physiology or disease state on drug ADME
• Explaining the drug interactions

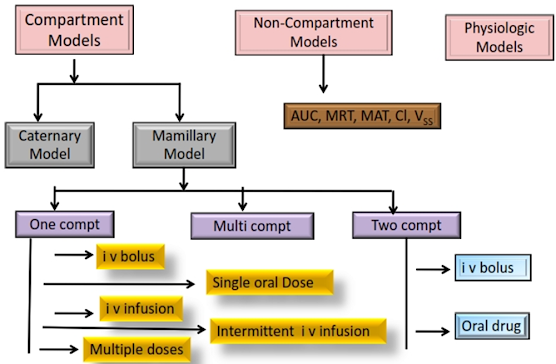
Compartment models

• Compartment Models also called Empirical models
• The compartmental analysis is the traditional and most commonly used approach to the pharmacokinetic characterization of a drug
• These models simply interpolate the experimental data and allow an empirical formula to estimate the drug concentration with time
• A compartment is not real but an imaginary & hypothetical one
• The body is composed of several compartments that are connected reversibly to each other
• The kinetics of drugs can be explained by modeling
• The rate of drug movement b/w compartment follows first-order kinetics

Advantages

• Visual representation of various rate processes involved in drug disposition
• Possible to derive equations describing drug concentration changes in each compartment
• Possibility of estimating the amount of drug in any compartment of the system after the drug is introduced into a given compartment

Disadvantages

• The concentration of some drugs cannot be predicted well though blood levels can be predicted easily
• Compartment behavior may change with the route of administration

Types of compartments

• Highly perfused organs – Central compartment
• Poorly perfused organs – peripheral compartment

Assumptions of compartmental models

• The body is represented as a series of compartments arranged in series or parallel to each other
• The rate of drug movement between compartments is described by first-order kinetics
• Rate constants are used to represent the rate of entry into and exit from the compartment
• A statistical analysis of plasma concentration-time data is another method used to find out no.of compartments
• Within each compartment, the drug is considered to be rapidly and uniformly distributed i.e. the compartment is well-stirred

Pharmacokinetic Modelling

 

Caternary model

• In this model, the compartments are joined to one another in a series like the compartments of a train.

• This is however not observable physiologically/anatomically as the various organs are directly linked to the blood compartment.

• Hence this model is rarely used

Catenary model

• The number of rate constants that will appear in a particular compartment model is given by R.

• For intravenous administration

R = 2n – 1

For extravascular administration,

R = 2n

where n = number of compartments

Applications of Pharmacokinetic Models

• Characterizing the behavior of drugs in patients

• Predicting the multiple-dose concentration curves from single-dose experiments

• Calculating the optimum dosage regimen for individual patients

• Evaluating the risk of toxicity with certain dosage regimens. Correlating plasma drug concentration with pharmacological response

• Estimating the possibility of drug and/or metabolite(s) accumulation in the body

• Explaining drug interactions

Assumptions

One Compartment Open Model

(Instantaneous Distribution Model)

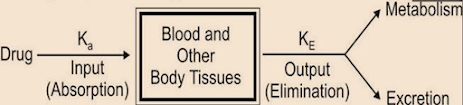
• The body is considered a single, kinetically homogenous unit that has no barriers to the movement of drug

• Simplest model

Estimation of Pharmacokinetic Parameters – IV Administration

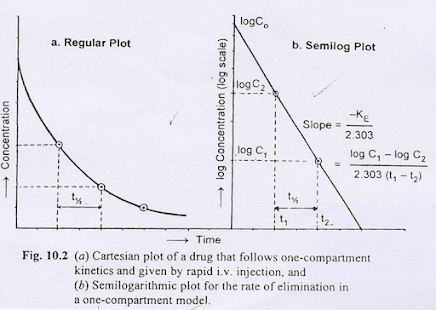
• The drug that follows one compartment kinetics administered as rapid i.v injection, the decline in plasma drugs level is only due to the elimination of the drug from the body (not due to distribution), the phase is called the elimination phase
• The elimination phase is characterized by 3 parameters

– Elimination rate constant

– Elimination half-life

– Clearance

Elimination Rate Constant

Integration of equation 3 yields

In X= In X_O – K_Et…………. (4)

• where X_O= Amount of drug at time t = zero i.e the initial amount of drug injected
• Equation 4 in the exponential form as

X = X_Oe-^KE^t…………..(5)

• The above equation shows that the disposition of a drug that follows one-compartment kinetics is monoexponential
• Transforming equation 4 into common logarithms:

log X = log X₀ – K_Et/ 2.303 ……………(6 )

• Since it is difficult to determine directly the amount of drug in the body X, a direct relationship exists b/w plasma C and X, thus

X = V_dC………………….(7 )

• Where Vd = proportionality constant or apparent volume of distribution
• If the PK parameter allows the use of plasma drug conc. in place of the amount of drug in the body, the equation becomes

log C = log C₀ – K_Et / 2.303  …………….(8)

• C0 = plasma drug concentration immediately after i.v injection

The elimination of the drug from the body is the sum of:

• Urinary excretion
• Metabolism
• Biliary excretion
• Pulmonary excretion
• Other mechanisms are involved.

Overall elimination rate constant (KE)

K_E = K_e + K_m + K_b + K_P + ……………….(9)

• Drugs eliminated by a particular route can be evaluated if the number of rate constants is involved & these values are known.

Ex: If the drug is eliminated by urinary excretion & metabolism only, then the fraction of the drug excreted & fraction metabolized Fe, Fm can be given as

F_e = K_e/K_E,  …………….(10 a)

F_m = K_m/K_E,  ……………..(10 b)

Elimination Half-Life

• Also called a biological half-life
• It is one of the oldest, best-known, important PK parameters of the drug
• It is defined as the amount of drug in the body as well as plasma concentration to decline by one-half or 50 % of its initial value
• Half-life is related to the elimination rate constant by the following equation

t_1/2 = 0.693/K_E ………………( 11)

• But half-life is a secondary parameter that depends upon primary parameters like clearance & apparent volume of distribution

t_1/2 = 0.693 V_d /Cl_T  ……………(12)

Apparent Volume of Distribution

• The apparent volume of distribution & Clearance are related to the physiological mechanisms in the body hence they are called primary parameters

V_d = X / C …………..(13)

• Vd is the measure of the extent of distribution of drugs expressed in liters
• The simplest way to determine Vd by rapid i.v injection is by determining the plasma conc. immediately

V_d = X₀ / C₀ = i.v bolus dose / C₀……………..(14)

• It can be used for drugs that obey one-compartment kinetics. But the non-ompartmental model can be applied to many compartmental models for estimating Vd
• For drugs given as i.v bolus,

V_d = X₀ / K_EAUC……………..(15 a)

• For drugs given by e.v

V_d(area)  = FX₀ / K_EAUC…………(15 b)

Where

X0 = dose administered

F = fraction of drug absorbed into the systemic circulation

F = 1, when the drug is administered by i.v route

Compartment Modelling Intravascular and Extravascular Summary

• The body is composed of several compartments that are connected reversibly to each other
• The kinetics of drugs can be explained by modeling
• Types of compartments are Central compartment and peripheral compartment
• One compartment applies only to those drugs which are rapidly distributed throughout the body
• The term open indicates that input (availability) & output (elimination) are unidirectional
• If the drug is not removed from the body then the model refers as a closed model
• Different forms of one-compartment open models based on the rate of input are one-compartment open model IV bolus administration, a one-compartment open model for continuous IV infusion, extravascular administration Zero order absorption, and extravascular administration first-order absorption

Compartment Modelling Intravascular and Extravascular PDF Notes Download

Compartment Modelling Intravascular and Extravascular